|
Stap 1 | Stap 2 | Stap 3 | Stap 4 | Stap 5 | Stap 6 | volgende pagina | vorige pagina Schaakcomputers worden steeds beter. Een zakschaakcomputer uit de speelgoedwinkel speelt al sterker dan een grootmeester. Een beetje frustrerend is het wel, dat je na jaren schaakstudie van een stuk kinderspeelgoed moet verliezen. Tien jaar geleden waren schaakcomputers nog niet zo goed, maar ook toen al wonnen ze van sterke clubschakers. Nog verder terug in de tijd, in 1980, bestonden schaakcomputers nog maar net. Ze konden er toen niet veel van en iedereen moest lachen om de sullige zetten van de computer die met een biepje werden aangekondigd. Men geloofde niet dat een schaakcomputer ooit van de wereldkampioen zou winnen. Hoe zou de mens ook ooit verslagen kunnen worden door iets dat hij zelf heeft uitgevonden? In die tijd sloten schakers en computerdeskundigen weddenschappen af over de vraag of een schaakcomputer vóór het jaar 2000 de wereldwereldkampioen zou verslaan. In dit verhaal lees je wie de weddenschap won. Je kunt zeggen dat een schaakcomputer over een stelling nadenkt, net als mensen. Het ligt er wel aan wat je onder denken verstaat. We weten niet goed hoe onze hersenen werken, dus ook niet hoe mensen denken. Maar wel weten we precies hoe een schaakcomputer denkt. Een schaakcomputer is een rekenmachine die razendsnel getallen bij elkaar optelt en aftrekt. De computer rekent aan schaakstellingen alsof het getallen zijn. Elke schaakstelling krijgt een waarde, een soort rapportcijfer. Staat wit bijvoorbeeld een loper voor, dan krijgt de stelling de waarde 3 omdat een loper 3 punten waard is. Staat het gelijk, dan krijgt de stelling de waarde 0. Als wit alle stukken van zwart slaat en zelf niets verliest, dan heeft de stelling de waarde 39. Reken maar uit. Een nog hogere waarde krijg je als wit al zijn pionnen laat promoveren tot dame. De waarde van alle witte stukken tezamen is dan 103. Is dit al de hoogste waarde? Nee, er is een uitzondering. Als het schaakmat staat, dan heeft de stelling een nog hogere waarde. Dit betekent dat mat geven de allerbeste zet is. Vanwege de hoge waarde van de koning zal een schaakcomputer nooit zijn koning wegeven en altijd netjes schaak opheffen. Maar hoe weet een schaakprogramma hoe de schaakstukken bewegen? Ook daarvan kun je met eenvoudige rekenregels een voorstelling maken. Elke stuk heeft zijn eigen regels die lijken op optellen en aftrekken. 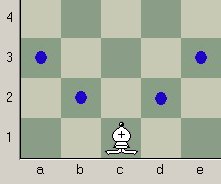 Eenvoudige rekenregels voor de witte loper op veld c1 Schuin rechts naar boven: De loper mag naar veld d2 want c+1=d en 1+1=2 De loper mag naar veld e3 want c+2=e en 1+2=3 Algemeen: de loper mag naar veld (c+x),(1+x) [maar (c+x) en (1+x) mogen beide niet groter zijn dan 8] Schuin links naar boven: De loper mag naar veld b2 want c-1=b en 1+1=2 De loper mag naar veld a3 want c-2=a en 1+2=3 Algemeen: de loper mag naar veld (c-x)(1+x) [(c-x) mag niet kleiner zijn 1 en (1+x) niet groter dan 8] Hoe zien de regels voor de loper er uit met een zwarte toren op b2? Hoe zien de regels er met een wit paard op c1? Een schaakprogramma kent dus de loop en de waarde van de stukken en het weet wat mat is. Meer kennis heeft het programma niet nodig. Het programma berekent de waarde van alle stellingen die ontstaan na elke mogelijke zet van wit. Is de waarde van de nieuwe stelling groter geworden, dan heeft het programma een goede zet gevonden, een zet die iets wint. Is de waarde kleiner geworden, dan is die zet juist slecht. In de eerste ronde van het onderzoek berekent het schaakprogramma alleen de mogelijke zetten van wit en het kijkt niet wat zwart kan antwoorden. In een bepaalde stelling zijn er bijvoorbeeld 40 mogelijke zetten van wit. De zet met de hoogste waarde is voorlopig de beste zet. De computer zal bijvoorbeeld een toren slaan omdat daar de hoogste winst ligt. Dit is al een mooi resultaat. Maar het is lang niet altijd goed om een toren te slaan. Er komt een tweede onderzoeksronde. Nu worden alle mogelijke zetten van zwart bekeken. In de tweede ronde moet de computer al veel meer rekenwerk verrichten. Want bij alle 40 zetten van wit zijn er ook steeds ongeveer 40 zetten van zwart (het kunnen er ook meer of minder zijn). Samen zijn dat 40 x 40 = 1600 mogelijkheden die allemaal berekend moeten worden. Maar omdat computers zo snel zijn, is de tweede ronde in een duizendste van een seconde doorlopen. Op de tweede zet zal de computer bijvoorbeeld 'zien' dat het niet goed is om de toren te slaan, omdat zwart dan bijvoorbeeld een dame van wit kan slaan. Een andere eerste zet van wit heeft nu de hoogste waarde gekregen, bijvoorbeeld de rokade. Maar het onderzoek is nog niet klaar. Er komt een derde ronde. Alle mogelijkheden worden nu bekeken na een zet van wit en een zet van zwart. Wit is weer aan de beurt. De zoekdiepte is nu 3 zetten (3 ply zeggen ze). Bij elk van de 1600 stellingen uit de tweede ronde zijn er weer ongeveer 40 mogelijkheden voor wit. Dat zijn 40 x 40 x 40 = 64.000 stellingen. Nog steeds is dat voor een computer een fluitje van een cent, waarvoor veel minder dan een seconde nodig is. In deze derde ronde kan blijken dat het toch goed is om de toren te slaan, omdat wit op de 3e ply, wanneer zwart een dame slaat, zelf ook een dame kan slaan. Samen met de torenwinst op de 1e ply is dat weer voordelig. Maar nog is het onderzoek niet klaar.  De boom van mogelijkheden na drie ronden (3 ply) http://entertainment.howstuffworks.com/chess1.htm Er komt een vierde ronde. Alle stellingen worden onderzocht na twee zetten van wit en twee zetten van zwart (samen 4 ply). Hiervoor zijn 40 x 40 x 40 x 40 = 2.560.000 berekeningen nodig. Een gigantische hoeveelheid zetten. Maar een snelle PC heeft hiervoor slechts een seconde nodig. Als je de computer een kleine minuut laat denken, dan is ook de vijfde ply voltooid. Er zijn nu honderdmiljoen stellingen berekend. De computer weet van alle mogelijke zetten welke zetten voor wit en welke voor zwart de meest gunstige zijn. De stelling met de hoogste waarde voor wit is de zet die de computer speelt. Als het programma nu maar lang genoeg doorrekent kan het zijn dat het ziet dat de toren toch niet geslagen mag worden vanwege mat op de 6e ply, of nog dieper, ergens op de 10e ply. Zo ongeveer werkt een schaakcomputer (1). Om een paar zetten diep te rekenen moet er dus heel veel werk gedaan worden. Computers schaken dus anders dan mensen. Computers maken ook andere fouten dan mensen. Toch is het interessant dat het schaakdenken kan worden vervangen door een paar eenvoudige rekenregels. Wist je trouwens dat computers alleen maar met de cijfers 1 en 0 rekenen? (Hoe dat werkt is weer een ander verhaal.) Misschien dat de computer de mens uiteindelijk op elk terrein zal overtreffen, als hij maar snel genoeg is... Een menselijke schaker die een minuut nadenkt, ziet tussen de 10 en 100 stellingen. Mensen zijn dus zeer in het nadeel als ze spelen tegen een schaakcomputer. Maar mensen hebben wel meer kennis van het schaakspel. Een schaker uit Stap 1 weet bijvoorbeeld al dat het goed is om de stukken te ontwikkelen. En in Stap 3 leer je de sleutelvelden. Met die kennis zie je in een oogwenk dat een bepaald pionneneindspel gewonnen is. Een computer heeft die kennis niet en moet alle mogelijkheden van het pionneneindspel uitrekenen, ook de allerdomste. Soms zijn er miljarden berekeningen nodig om een simpele zet te vinden die ervaren schakers meteen zien. En dat is ook de reden waarom schakers lange tijd niet konden geloven dat schaakcomputers ooit goed zouden worden. Computerprogrammeurs hebben nooit een goede manier gevonden om meer schaakkennis in een programma te stoppen. Niet dat dit onmogelijk is. Maar de rekensnelheid van het programma zou door die extra kennis enorm afnemen. Kennis is voor een computer dus eigenlijk ballast. Het nadeel van kennis is groter dan het voordeel. Maar misschien dat ergens in de toekomst, als computers weer veel sneller zijn geworden, het opeens voordelig wordt om schaakkennis in de programma's te stoppen. Want de hoeveelheid verspilde arbeid aan een steeds hoger percentage nutteloze zetten neemt met elke ply explosief toe. Op dit moment is het nog zo dat schaakprogramma's niet te veel mogen weten. Het interessante is dat ze met weinig kennis toch hun stukken ontwikkelen en ook de sleutelvelden vinden, ook al hebben ze geen idee wat 'sleutelvelden' zijn. Een goede zet bedenken is een zoekproces. Dit geldt zowel voor mensen als voor computers. Stel, je raakt op school je fietssleutel kwijt. Dan ga je zoeken. Als je slim zoekt, dan kijk je alleen op plaatsen waar je geweest bent en je probeert te beredeneren waar de sleutel moet liggen. Je zoekt eerst op de meest voor de hand liggende plekken, en liefst ook op plaatsen waar je meteen bij kunt: in je broekzak of in je tas. Zo zoeken mensen. En dat is slim. Maar een computer kan niet redeneren. Hij zoekt systematisch op alle plaatsen in de hele school, in de prullenbak, in de bloempotten, op de wc, achter het schoolbord en zelfs in het gymlokaal, ook al ben je daar niet geweest. Niet erg slim dus. Maar omdat computers zo snel zijn, vindt een fietssleutelzoekcomputer de sleutel toch meestal eerder. Tenzij de sleutel toevallig in je broekzak zit! Zo is het ook met schaakcomputers. Snelheid heeft het gewonnen van slimheid. Schaakcomputers blijven dus erg dom. En dat zie je aan de manier waarop ze schaken. Je zou best kunnen volhouden dat schaakcomputers van het schaakspel nog steeds niets begrijpen. Het slimme zit hem vooral in het inzicht dat veel dom werk toch een slim resultaat kan opleveren. Dit is een typisch menselijk inzicht. Computers zelf weten dat helemaal niet. Daar zijn ze nu juist te dom voor. Deep Blue, de schaakcomputer van het computerbedrijf IBM, was speciaal gemaakt om de wereldkampioen te verslaan. Het programma kon tweehonderd miljoen stellingen per seconde aan. In 1997, drie jaar vóór het jaar 2000, speelde een soort klerenkast van 1400 kilo, vol met parallelle processoren, een match van zes partijen tegen Garry Kasparov, volgens sommigen de beste schaker die ooit geleefd heeft. De klerenkast won: 3½-2½. Vanwege de weddenschappen moesten overal ter wereld schakers grote geldbedragen aan computerdeskundigen overmaken.  Deep Blue: 200.000.000 stellingen per seconde Hoogte: tot aan het plafond - Gewicht: 1400 kg Tot op de dag van vandaag kan Kasparov niet geloven dat hij is verslagen door een stuk rekentuig. Na de match dacht hij zelfs dat er oneerlijk spel was gespeeld en eiste een revanche. Ook eiste hij een uitdraai van de zetten die de computer had berekend omdat hij het niet vertrouwde. Dit laatste was een onmogelijke eis. Er zou een rol van honderden kilometers papier nodig zijn om alle berekeningen van de schaakcomputer uit te printen! En zelfs als je die gigantische rol kettingpapier per vrachtwagen thuisbezorgd kreeg, kon je daarmee niets beginnen. Waar moest je in hemelsnaam beginnen met het controleren van die eindeloze rij getalletjes? De uitdraai heeft Kasparov niet gekregen. De revanchematch ook niet. Meteen na de match werd de computer uit elkaar geschroefd en gebruikt voor nuttiger doeleinden dan het spelen van een spelletje schaak. Misschien dat de gegevens op het belastingformulier van je vader nu ergens in het magnetisch geheugen van Deep Blue bewaard worden. Kasparov bleef boos en je hoort hem zo nu en dan nog mopperen op IBM. De mensen van de computerfabriek waren juist zeer in hun nopjes. Wereldwijd hadden miljoenen de match gevolgd. Wat een publiciteit had dat opgeleverd. Het nieuws haalde alle voorpagina's. Wat vond Deep Blue eigenlijk zelf van zijn overwinning? Was het schaakprogramma blij dat het gewonnen had? Nee. Deep Blue kan namelijk wel snel denken, maar gevoel heeft een schaakcomputer niet. Computers weten niet eens dat ze bestaan, als je het mij vraagt. Links computerschaak |